CPSC 352 -- Artificial Intelligence
Notes: Heuristic Search
Source: G. Luger, Artificial Intelligence, 4th edition, Chapter 3
Introduction
According to George Polya heuristics is the study of the methods and rules of discovery and invention. In state space search, heuristics define the rules for choosing branches in a state space that are most likely to lead to an acceptable solution. There are two cases in AI searches when heuristics are needed:- The problem has no exact solution. For example, in medical diagnosis doctors use heuristics to choose the most likely diagnoses given a set of symptoms.
- The problem has an exact solution but is too complex to allow for a brute force solution.
Key Point: Heuristics are fallible. Because they rely on limited information, they may lead to a suboptimal solution or to a dead end.
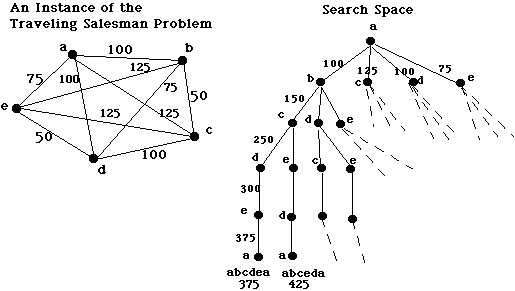
Example: The traveling salesman problem is too complex to be solved via exhaustive search for large values of N. The nearest neighbor heuristic work well most of the time, but with some arrangements of cities it does not find the shortest path. Consider the following two graphs. In the first, nearest neighbor will find the shortest path. In the second it does not:

Example: Consider the game of tic-tac-toe. Even if we use symmetry to reduce the search space of redundant moves, the number of possible paths through the search space is something like 12 x 7! = 60480. That is a measure of the amount of work that would have to be done by a brute-force search.
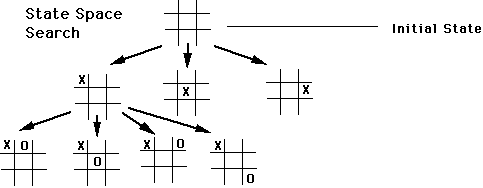
Simple heuristic for tic-tac-toe: Move to the square in which X has the most winning lines. Using this rule, we can see that a corner square has heuristic value of 3, a side square has a heuristic value of 2, but the center square has a heuristic value of 4. So we can prune the left and right branches of the search tree. This removes 2/3 of the search space on the first move. If we apply the heuristic at each level of the search, we will remove most of the states from consideration thereby greatly improving the efficiency of the search.
Implementation: Heuristic search is implemented in two parts:
- The heuristic measure.
- The search algorithm.
Best First Search
The best first search algorithm uses an open list to keep track of the current fringe of the search, and a closed list to keep a record of states already visited. On the open list, the states are ordered according to some heuristic estimate of the closeness to the goal:
procedure best_first_search {
open := [Start]; % Initialize
closed := [];
while open != [] do { % While states remain
remove the leftmost state from open, call it X;
if X = goal then return path from Start to X;
else {
generate children of X;
for each child of X do
case {
the child is not on open or closed: {
assign the child a heuristic value;
add the child to open;
}
the child is already on open: {
if this child was reached by a shorter path
then give the state on open the shorter path
}
the child is already on closed: {
if this child was reached by a shorter path {
then remove the state from closed;
add this child to open;
}
}
} % cases
put X on closed;
re-order states on open by heuristic merit (best leftmost)
} % else
} % while
return failure % open is empty
} % best_first
Example: Consider the following hypothetical search space and the trace of the best-first-search algorithm on it. The numbers associated with the state names give the heuristic value of the state.

Heuristic Evaluation Functions
Recall the 8-puzzle:

- Heuristic 1 (H1) : Count the out-of-place tiles, as compared to the goal.
- Heuristic 2 (H2): Sum the distances by which each tile is out of place.
- Heuristic 3 (H3): Multiply the number of required tile reversals by 2.
Weaknesses
- H1 doesn't account for the distance that tiles have to move to get in place.
- H2 doesn't account for tile-reversals. It takes several moves to reverse two adjacent tiles.
- H3 often fails to distinguish between vastly different states.
Example: Consider the following example:
Start Goal H1 H2 H3
----- ---- -- -- --
2 8 3 1 2 3
1 6 4 8 - 4 5 6 0
- 7 5 7 6 5
2 8 3 1 2 3
1 - 4 8 - 4 3 4 0
7 6 5 7 6 5
2 8 3 1 2 3
1 6 4 8 - 4 5 6 0
7 5 - 7 6 5
Key Point: Developing good heuristics is a difficult, empirical (trial and error) process. The final measure of a heuristic's value is its actual performance on the search problem.
Analysis of the Evaluation Function
In developing a good evaluation function for the states in a search space, you are interested in two things:- g(n): How far is state n from the start state?
- h(n): How far is state n from a goal state?
The first value, g(n), is important because you often want to find the shortest path. This value (distance from start) can be exactly measured by incorporating a depth count into the search algorithm.
The second value, h(n), is important for guiding the search toward the goal. It is an estimated value based on your heuristic rules.
Evaluation function. This gives us the following evaluation function:
f(n) = g(n) + h(n)
where g(n) measures the actual length of the path from the start state to the state n, and h(n) is a heuristic estimate of the distance from a state n to a goal state.
Heuristic Applied to the Eight Puzzle
The following figure shows the full best-first search of the eight puzzle graph using H1 -- that is, the value of h(n) is the number of tiles out of place. The number at the top of each state represents the order in which it was taken off of the open list. The levels of the graph are used to assign g(n). For each state, its heuristic value, f(n) is shown.

Note the tie that occurs in step 3, where E and F have the save value. State E is examined first, which puts its children, H and I, on the open list. But since state f(F) has a lower value than f(H) and f(I), the search is prevented from going down to those children. In effect, the g(n) gives the state more of a breadth-first flavor, keeping it from going too deeply down paths that don't get near a goal.
Summary.
- Operations on states generate children of the state currently being evaluated.
- To prevent loops, Each new state is checked to see whether it occurred before.
- Each state, n, is given an f value, using f(n) = g(n) + h(n), where h guides the search toward promising states and g prevents it from going too far on a dead end.
- States on open are sorted by their f values.
- Efficiency can be improved by efficient management of the open and closed lists.
0 comments:
Post a Comment